H5分层屏幕适配公式推导
转载请注明出处:http://hai.li/2018/03/14/h5-screen-adaptation-formula-derivation.html
此文为 h5 屏幕适配具体公式推导,原理和使用参考 http://hai.li/2018/03/14/h5-screen-adaptation.html
缩放
有时我们需要的是设计稿宽高比 v/g 大于屏幕宽高比 u/f 时设计稿宽 v1 等于屏幕宽 u ,否则设计稿高 g1 等于屏幕高 f。求满足要求得设计稿缩放值 s ?
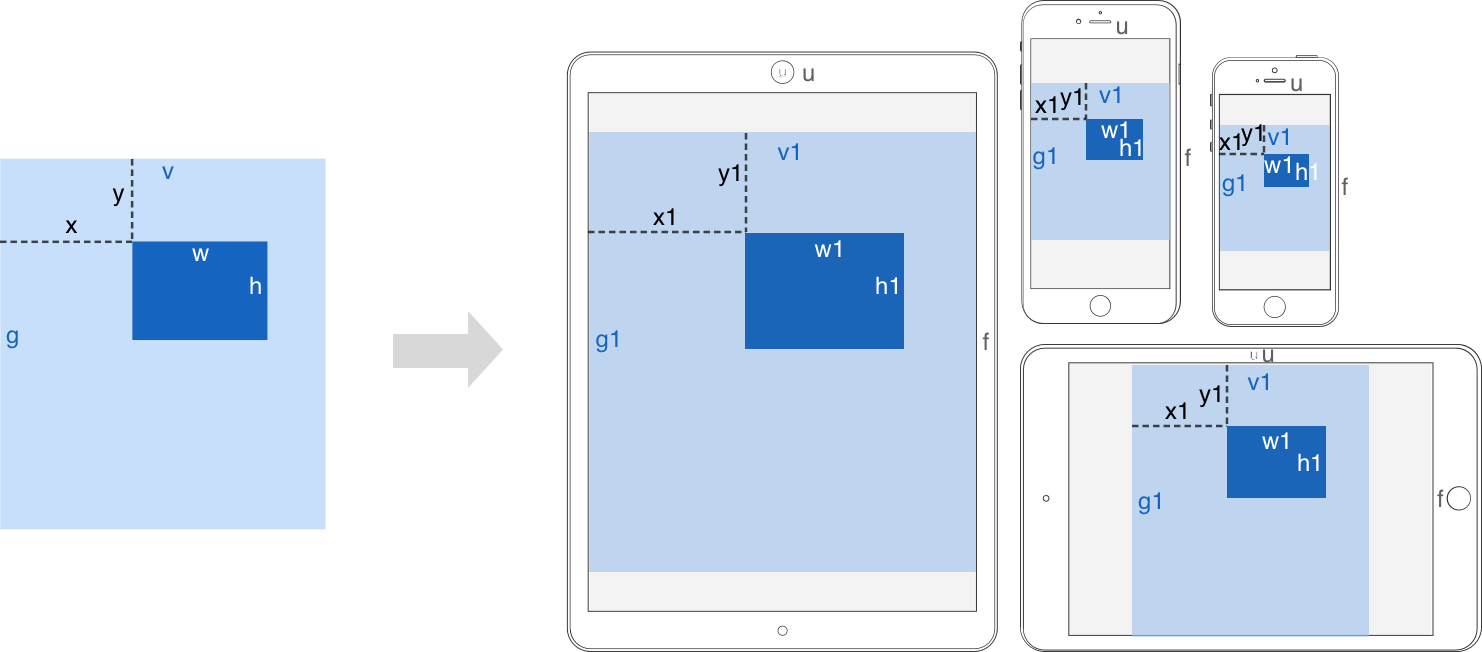
由条件可得
x1 = x*s
y1 = y*s
v1 = v*s
g1 = g*s
w1 = w*s
h1 = h*s
当 v/g >= u/f 时 两边乘 f/v 得
f/g >= u/v
由 v1 = u 得
v1 = v*s
= u
s = u/v
即 f/g >= u/v 时 s = u/v
当 v/g < u/f 时 两边乘 f/v 得
f/g < u/v
由 g1 = f,得
g1 = g*s
= f
s = f/g
即 f/g < u/v 时 s = f/g
即 s 为 f/g 和 u/v 最小值
即设计稿缩放值 s = Math.min(f/g, u/v)
内存优化
如果每一层都是宽 v1 高 g1,层数一多,占用 gpu 内存就非常多,特别是需要做 css 动画时,大内存会导致动画卡顿,应当减小推到 gpu 内存的层实际面积减少内存占用。 如果拉伸设计稿 v*g 至 屏幕 u*f 大小,对应 w*h 区域坐标变成 (x3, y3),宽高变成 w3*h3 ,假设此时横向拉伸 sx 纵向拉伸 sy 。
由条件得
u = v*sx
f = g*sy
x3 = x*sx
y3 = y*sy
w3 = w*sx
h3 = h*sy
进而得
sx = u/v
sy = f/g
x3 = x*u/v
y3 = y*f/g
w3 = w*u/v
h3 = h*f/g
内存优化
(w3*h3)/(v1*g1) = ((w*u/v)*(h*f/g))/(v*s*g*s)
= w*u*h*f/(v*v*g*g*s*s)
当 v/g >= u/f 时
v1 = v*s = u
u = v*sx
得 s = sx = u/v
w3 = w*sx
= w*s
= w1
(w3*h3)/(v1*g1) = w*u*h*f/(v*v*g*g*s*s)
= w*h*f/(g*g*u)
由 v/g >= u/f
得 g/v <= f/u
得 g/v*(w*h/(g*g) <= f/u*(w*h/(g*g))
得 w*h/(v*g) <= w*h*f/(g*g*u)
得 (w3*h3)/(v1*g1) >= w*h/(v*g)
当 v/g < u/f 时
g1 = g*s = f
f = g*sy
得 s = sy = f/g
h3 = h*sy
= h*s
= h1
(w3*h3)/(v1*g1) = w*u*h*f/(v*v*g*g*s*s)
= w*u*h/(v*v*f)
由 v/g < u/f
得 v/g*(w*h/(v*v) < u/f*(w*h/(v*v))
得 w*h/(v*g) < w*u*h/(v*v*f)
得 (w3*h3)/(v1*g1) > w*h/(v*g)
即 (w3*h3)/(v1*g1) >= w*h/(v*g)
当 v/g >= u/f 时 v1 = u 且 w1 = w3
当 v/g < u/f 时 g1 = f 且 h1 = h3
所以可以构造出一个更小的层 w3*h3 且满足 w3 = w*u/v h3 = h*f/g ,元素在该区域内的保持不变形缩放,即可和设计稿整体在屏幕内缩放导致元素缩放一致。
如果仅将区域 w1*h1 推到 gpu 内存,则内存占用率达到最低点,相比推 v1*g1 减少了 1 - (w1*h1)/(v1*g1) = (w*h)/(v*g),而推 w3*h3 次之,减少了 1 - (w3*h3)/(v1*g1) <= 1 - w*h/(v*g)。 以 w = 544 h = 142 v = 1080 g = 1920 为例,推 w1*h1 减少了约 96.27%,而推 w3*h3 最多减少约 96.27% gpu 内存占用。
定位
缩放后还需要确定在容器中的定位,常见的就是贴边和居中。实际上就是求元素贴边或居中的坐标 (x2, y2)
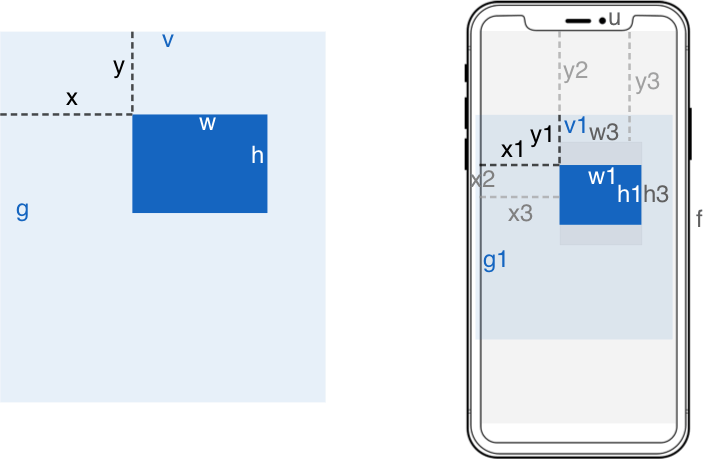
已知设计稿宽 v 高 g ,其中任意元素的宽 w 高 h 和坐标 (x, y) ,横向左留白占总留白的比值为 m ,纵向上留白占总留白的比值为 n,假设设计稿尺寸到实际尺寸缩放了 s 倍,求经过屏幕适配后该元素的实际宽 w2 高 h2和坐标(x2, y2)?
由条件可得
x1 = x*s
y1 = y*s
v1 = v*s
g1 = g*s
w1 = w*s
h1 = h*s
m = x2/(u - v1)
n = y2/(f - g1)
继而得
y2 = n*(f - g1)
= n*(f - g*s)
= n*f - n*g*s
y2 + y1 = n*f - n*g*s + y1
= n*f - n*g*s + y*s
= n*f + (y - n*g)*s
= n*f + (y - n*g)/h*h*s
= n*f + (y - n*g)/h*h1
同理
x2 = m*(u - v1)
= m*(u - v*s)
= m*u - m*v*s
x2 + x1 = m*u - m*v*s + x1
= m*u - m*v*s + x*s
= m*u + (x - m*v)*s
= m*u + (x - m*v)/w*w*s
= m*u + (x - m*v)/w*w1
background-size 实现
假设对于区域 w3*h3, 求 w3*h3 内横向上左留白 x2 + x1 - x3 占总留白 h3 - h1 比值 p 和纵向上上留白 y2 + y1 - y3 占总留白 w3 - w1 比值 o?
已知
x3 = x*u/v
y3 = y*f/g
w3 = w*u/v
h3 = h*f/g
p = (y2 + y1 - y3)/(h3 - h1)
o = (x2 + x1 - x3)/(w3 - w1)
得 p = (n*f - n*g*s + y*s - y*f/g)/(h*f/g - h*s)
= (n*(f - g*s) + y*(s - f/g))/(h*(f/g - s))
= n*(f - g*s)/(h*(f/g - s)) + y*(s - f/g)/(h*(f/g - s))
= n*(f - g*s)/(h/g*(f - g*s)) - y*(f/g - s)/(h*(f/g - s))
= n*g/h - y/h
= (n*g - y)/h
同理
o = m*v/w - x/w
= (m*v - x)/w
svg 标签实现
已知 h3 = h*f/g
得 f = h3*g/h
y2 + y1 = n*f - n*g*s + y*s
= n*h3*g/h + (y - n*g)*s
= n*g/h*h3 + (y - n*g)/h*h*s
= n*g/h*h3 + (y - n*g)/h*h1
同理
已知 w3 = w*u/v
得 u = w3*v/w
得 x2 + x1 = m*v/w*w3 + (x - m*v)/w*w1
方案完善
上面以刚好全部显示的屏幕适配方案,同理可推导刚好占满适配及拉伸适配
占满适配屏幕
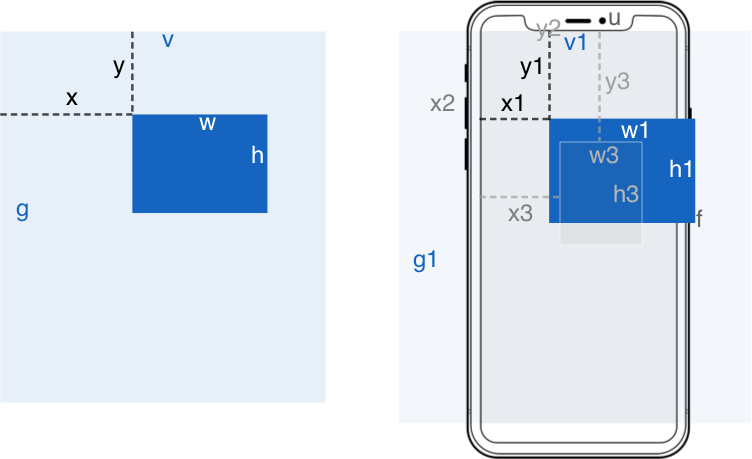
原理
设计稿缩放值 s = Math.max(f/g, u/v)
内存优化 (w3*h3)/(v1*g1) >= w*h/(v*g)
当 v/g < u/f 时 v1 = u 且 w1 = w3
当 v/g >= u/f 时 g1 = f 且 h1 = h3
x1 = x*s
y1 = y*s
w1 = w*s
h1 = h*s
v1 = v*s
g1 = g*s
横向上左超出占总超出比值 m = x2/(v1 - u)
贴屏幕顶时 m = 0
垂直居中时 m = .5
贴屏幕顶时 m = 1
纵向上上超出占总超出比值 n = y2/(g1 - f)
贴屏幕左时 n = 0
水平居中时 n = .5
贴屏幕右时 n = 1
x2 = m*(v1 - u)
= m*v*s - m*u
y2 = n*(g1 - f)
= n*g*s - n*f
x1 - x2 = m*u - m*v*s + x*s
= m*u + (x - m*v)/w*w1
= m*v/w*w3 + (x - m*v)/w*w1
y1 - y2 = n*f - n*g*s + y*s
= n*f + (y - n*g)/h*h1
= n*g/h*h3 + (y - n*g)/h*h1
x3 = x*u/v
y3 = y*f/g
w3 = w*u/v
h3 = h*f/g
o = (x3 - x1 + x2)/(w3 - w1)
= (x - m*v)/w
p = (y3 - y1 + y2)/(h3 - h1)
= (y - n*g)/h